 
１．加算回路と減算回路
（かさん かいろ と げんざん かいろ）
2進数１桁の足し算では、すべての組み合わせは４とおりです。
足した結果には、1桁目の値と、桁上がりの値が必要です。
これを表にしてみましょう。
表1-1 2進数１桁の加算
| A |
B |
１桁目 |
桁上がり |
| 0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
1桁目と桁上がりを論理式で表現できないかを考えてみましょう。
AND、OR、NOTなどを使って、整理したものが表1-2です。
表1-2 加算を論理式で表現
| A |
B |
C = A and B |
D = A or B |
E = not C |
F = D and E |
| 0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
0 |
|
|
（桁上がり） |
|
|
（一桁目） |
一桁目の部分は、A＝Bのとき０、 A≠1のとき１となっています。
この演算を排他的論理和「EXOR(Exclusive OR)」とも呼び、
等しくないことを示す演算子でもあります。
表1-2から、１ビットの加算回路は次のようになることがわかるでしょう。
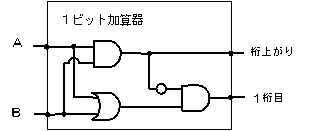
図1-1 １ビット加算器
1ビット以上になると、最下位ビット以外は、
下位からの桁上がりを更に加算しなければなりません。
だから、図1-2のように１ビット加算器が並ぶことになります。
（注意） 一般にNビットの加算では、N×（N＋１）／２個の
1ビット加算器が必要となります。
図1-2では、Aの各ビットをAｎ、Bの各ビットをBn、
結果をCｎと表記しています（n=0〜3）。
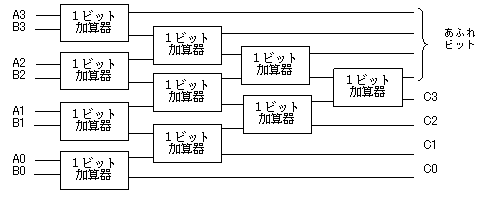
図1-2 4ビット加算器
10進数の世界で、私たちが引き算を行うとき、下位の桁から順にやります。
桁ごとに、順に大きさを比較し、引かれる数が引く数より大きければ、
そのまま引き、引かれる数が小さければ、上位桁から１０借りてきて・・・。
 |
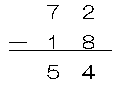@) １の位では２＜８だから、10の位から１０借りてくる。 |
| A） １０＋２から８を引いて４を1位の値とする。 |
| B） 下位から１０を借りられたので、７−１＝６とする。 |
| C） ６−１＝５を１０の位とする。 |
さて、いかにも複雑ですね。と思う人は少ないでしょうか？
ここでちょっと視点を変えてみます。
今、上位桁から借りてくるのを最初にやってしまいましょう。
まず、１００から１８を引きます。
答えは８２。
この計算は、つり銭の計算でよくやりますから、なれていますね。
この８２に７２を加えます。
７２＋８２＝１５４
最初，１００を借りていたのですから、１００を引いて５４となります。
１５４−１００＝５４
答えは、同じく５４になりました。
あるいは、2桁の大きい正の値から、
２桁の小さい正の値を引いたのですから、
２桁以上を無視すればよいわけです。
1.4 補数（ほすう）
１０進法で、計算の対象となっている数より大きい桁を持ち、
最上位が１で後は０の値、1.3の例で言えば１００のことですが、
この値から数を引いた値を１０の補数と呼びます。
たとえば、１８の１０の補数は８２です。
同様に２進法で、計算の対象となっている数より大きい桁を持ち、
最上位が１で後は０の値から、数を引いた値を２の補数と呼びます。
2進数では０か１しかありませんから、
実は、この値を簡単に求めることができます。
まず、単純に引いて２の補数を求めた値と、
引く数の各桁のビットを反転した値を比較してみましょう。
| [単純に引いた値] |
1 0000 0000 − 0000 1101 |
= 1111 0011 |
| [ビットを反転した値] |
0000 1101 の各ビット反転 |
= 1111 0010 |
|
|
|
| [単純に引いた値]
|
1 0000 0000 ? 0000 1010 |
= 1111 0110 |
| [ビットを反転した値] |
0000 1010 の各ビット反転 |
= 1111 0101 |
|
|
|
|
| [単純に引いた値] |
1 0000 0000 ? 0000 0001 |
= 1111 1111
|
| [ビットを反転した値] |
0000 0001 の各ビット反転 |
= 1111 1110
|
各桁のビットを反転した値は、
単純に引いた値より１だけ少ない値になっています。
ですから、ビット反転した値に１を加えて補数をつくることができるわけです。
ビットの反転はNOTだけの回路です。
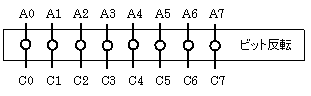
図1-3 ビット反転（8ビットのとき）
ビットを反転したあと、１を加算します。
この１の値としては、最下位ビットのみ１、
それ以外は0として加算器に入力すればよいわけです。
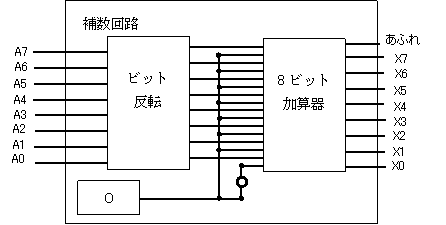
図1-4 ２の補数回路（8ビットのとき）
補数回路では、A0〜A7の全ビットが 0
のとき、あふれビットが発生します。
さて、引く値の２の補数をとり、引かれる値と加算し、
あふれビットを無視すれば、結果的に減算が行われたことになります。
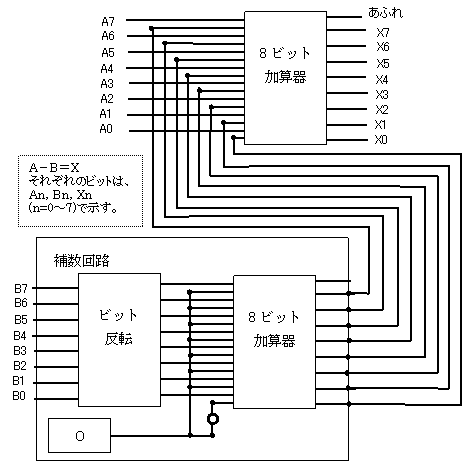
図1-5 8ビットにおける減算回路
|
１．加算回路と減算回路
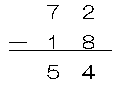
１． コンピュータは計算機