  
2.スイッチによる論理回路
(すいっち による ろんりかいろ)
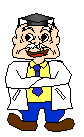
今まで出てきたスイッチの他に、スイッチ板がうすい鉄片でできていて、
その下に電磁石(でんじしゃく)があるようなスイッチを考えます。
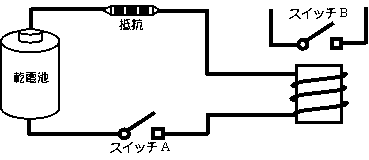
スイッチAをオンにすると、電磁石に電流が流れて、
鉄片でできたスイッチBは電磁石に引きよせられてオンになります。
スイッチAを切る(オフにする)と、同じようにスイッチBもオフになります。
まるで、スイッチのオン、オフの値がバトンタッチされ、
リレーしているみたいですね。
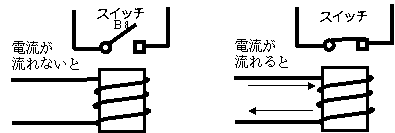
だから、このスイッチのことを「リレー」と呼びます。
さて、今度はスイッチBの鉄片が、電磁石側についていて、
電気が流れていないときは、スイッチはつながっている状態です。
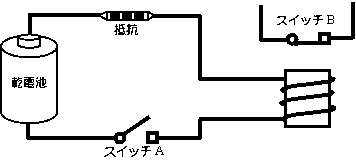
すなわち、スイッチAがオフになっているとき、
電磁石に電流が流れていないと、スイッチBはオンになっています。
スイッチAをオンにすると、電磁石に電流が流れて、
スイッチBの鉄片が電磁石に引きよせられてオフになります。
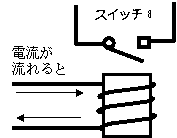 
スイッチAと逆の状態になります。
まるで「やれ」と言われたらやりたくないし、
「やるな」と言われたらやりたくなってしまう。
何か「あまのじゃく」のようなスイッチですね。
  
ここで、電流が流れればオンになり、
流れなければオフになるスイッチを「正スイッチ」、
電流が流れればオフになり、
流れなければオンになるスイッチを「逆スイッチ」と呼ぶことにします。
更に、今まで出てきた記号の他に、次のような記号を追加します。
その他の記号は、図1-1で示した記号を使います。

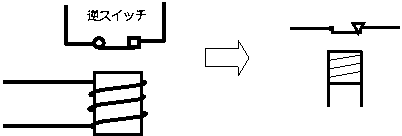
図2-1 正スイッチと逆スイッチの記号
  
(1) AND回路
次のような回路を考えてみましょう。
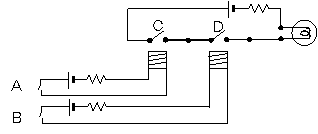
図2-2 スイッチによるAND回路
スイッチAがオフだと、Cの電磁石に電流が流れないので、
正スイッチCはオフです。
スイッチAをオンにすると、Cの電磁石に電流が流れて、
正スイッチはオンになります。
スイッチBと正スイッチDとの関係も同じようになります。
豆電球がつながっている方にも乾電池がありますので、
AとBがオン、すなわちCとDがオンになると豆電球が点灯します。
ところで、豆電球がついている側の回路だけをよく見てみましょう。
「1 豆電球による論理回路」で出てきたAND回路と、まったく同じですね。
(2) OR回路
次の回路はどうでしょう。
豆電球がついている側の回路は、正スイッチC、Dが並列になっています。
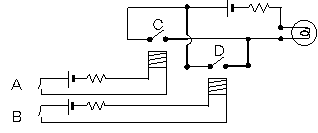
図2-3 スイッチによるOR回路
AまたはDがON、すなわちCまたはDがオンになると豆電球が点灯します。
だからOR回路となります。
(3) NOT回路
あまのじゃくの逆スイッチを使って次のような回路はどうでしょう。

図2-4 スイッチによるNOT回路
Aがオフのとき豆電球が点灯し、オンのとき消えます。
だからNOT回路となります。
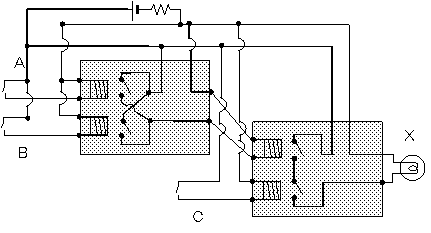
それでは、次のように、NOTをつないでみましょう。
図2-5 NOT(NOT A)回路
Aのスイッチがオフ(A=0)だったら、Cのスイッチがオンになり,
Dの近くの電磁石に電流が流れます。
Dは電磁石に引き寄せられてオフになり、豆電球Xはつきません(X=0)。
逆に、Aのスイッチがオン(A=1)だったら、
Cの近くの電磁石に電流が流れます。
Cは電磁石に引き寄せられてオフになります。
CがオフだとDの近くの電磁石には電流が流れませんので、
Dはオンのままです。
従ってDを含む回路に電流が流れ、豆電球が点灯します(X=1)。
すなわち、X=not(not A)=Aが成り立っていることになります。
  
図1-6と同じように、スイッチによる回路をパターン化します。
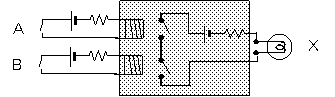
(a) AND回路
(b) OR回路

(c) NOT回路
(ハッチング部が、それぞれの回路のパターン)
図2-6 スイッチによる論理回路
豆電球側への線の出方は、NOTもAND、ORと同じです。
従って、線のつなぎ方による論理回路よりも単純です。
これらのパターンを使って、色々な回路を考えてみましょう。
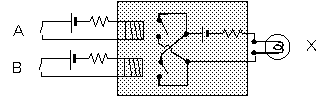
(a) X = (A or B) and C
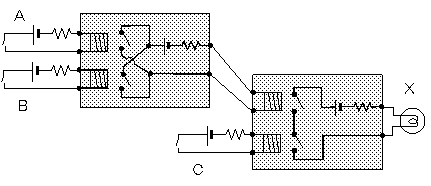
表2-1 (A or B) and Cの真理値表
| A |
B |
C |
A or B |
(A or B) and C |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
1 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
1 |
1 |
(b) X= not (A or B) (これをNORと呼ぶ)

表2-2 NORの真理値表
| A |
B |
A or B |
not(A or B) |
| 0 |
0 |
0 |
1 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
0 |
(c) X = not (A and B) (これをNANDと呼ぶ)
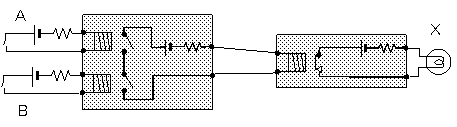
表2-3 NANDの真理値表
| A |
B |
A and B |
not(A and B) |
| 0 |
0 |
0 |
1 |
| 0 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
0 |
  
ところでANDやORのとき、正スイッチを直列や並列に並べました。
ちょっとためしに、逆スイッチを直列に並べてみましょう。
以下の回路で、スイッチAと逆スイッチCとは逆になります。
BとDの関係も同様です。
従って、真理値表は次のようになります。
| A |
B |
C=not A |
D=not B |
C and B |
| 0 |
0 |
1 |
1 |
1 |
| 0 |
1 |
1 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
0 |
結果が表2-2のNOR回路と同じになります。
ですから、次の式が成立することがわかります。
not (A or B) ≡ (not A)
and
(not B)
回路は、not(A or B)よりも単純になっています。
今度は、並列に並べてみましょう。

直列の場合と同じようにして、真理値表は次のようになります。
| A |
B |
C=not A |
D=not B |
C or B |
| 0 |
0 |
1 |
1 |
1 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
0 |
結果は表2-3のNAND回路と同じになります。
ですから、次の式が成立することがわかります。
not (A and B) ≡ (not
A) or
(not B)
2つの逆スイッチを使うことで、ひとつの結線だけですみ、
NOTとORを使った回路よりも簡単になりました。
  
実は、簡単化のために乾電池と抵抗を、
それぞれの素子に別々に入れていましたが、
実際には、これらは一緒にしてしまいます。
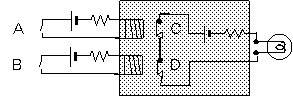
例えば、例題で、次のような回路がありました。

それぞれの素子に電源を持つことは無理なので、
実際の回路では、次のように、電源の部分を一ヶ所に集めてしまいます。
  
|

 2.スイッチによる論理回路
2.スイッチによる論理回路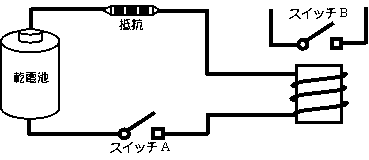
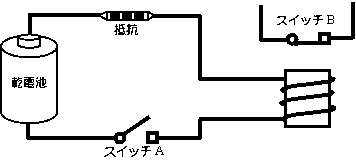



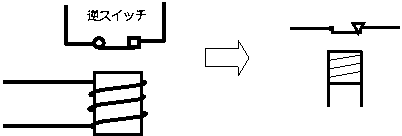












 1. コンピュータは計算機
1. コンピュータは計算機 2.コンピュータに必要な機能
2.コンピュータに必要な機能![]() 1.豆電球による論理回路
1.豆電球による論理回路 2.スイッチによる論理回路
2.スイッチによる論理回路 3.論理回路図の単純化
3.論理回路図の単純化 1.加算回路と減算回路
1.加算回路と減算回路 2.記憶回路
2.記憶回路 3.順序回路
3.順序回路![]()