
 1.豆電球による論理回路 1.豆電球による論理回路 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.1 | 乾電池(かんでんち)と豆電球(まめでんきゅう) |
| 1.2 | 回路図(かいろず)で使う記号(きごう) |
| 1.3 | AND(アンド)回路 |
| 1.4 | OR(オア)回路 |
| 1.5 | NOT(ノット)回路 |
| 1.6 | つなぎ方の工夫 |
| 1.7 | つなぎ方(結線)パターンの素子化 |
| 1.8 | NOTのつなぎ方で? |
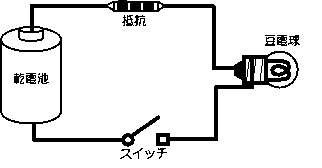
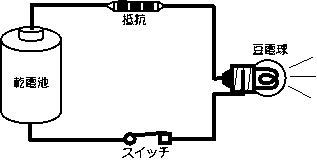
|
A |
B |
C |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
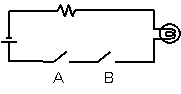
それでは、次のような回路ではどうでしょう。
スイッチA、Bが並列につながっています。
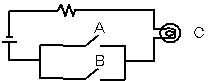
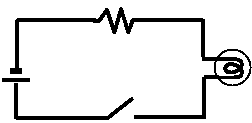
図1-4 OR回路(スイッチの並列)
この回路では、AとBのどちらかのスイッチがオンであれば、
豆電球Cは点灯します。
両方ともオフだったら、豆電球は点灯しません。
このことを、言葉で言えば、
「AまたはB(A or B)がオンならばCが点灯する」
ということができます。
ですから、この回路を「OR回路」と呼びます。
AND回路と同じように、スイッチがオフの状態を0、オンの状態を1、
豆電球が点灯していない状態を0、
点灯している状態を1として、真理値表にしてみましょう。
表1-2
ORの真理値表
|
A |
B |
C |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
次は、スイッチを1個だけ使います。次の回路を考えます。
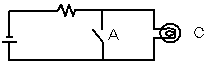
図1-5 NOT回路(結果の豆電球と並列)
この回路では、Aがオフであれば豆電球が点灯します。
オンだったらどうでしょう。
豆電球には抵抗がありますから、
Aをオンにすると豆電球の方には電流が流れません。
すなわち点灯しません。
ですから、
「Aがオンでなければ(not A)Cが点灯する」
ということができます。
ですから、この回路を「NOT回路」と呼びます。
NOT回路も真理値表で表現しましょう。
表1-3
NOTの真理値表
|
A |
C |
|
0 |
1 |
|
1 |
0 |
今までの3つの回路で、スイッチのオン、オフ(1または0)が入力、
豆電球が点灯する(1)か、しない(0)かを、出力として考えると、
3つの回路でAND、OR、NOT回路が実現できたことになります。
色々な論理演算は、最終的にはAND、OR、NOTで表現できますので、
これらの回路を使って、論理演算を表現できることになります。
これらのつなぎ方(結線)を工夫して、
色々な演算回路を作っていくわけです。
しかし、つなぎ方をその都度考えるのは大変です。
そこで、つなぎ方だけを、ひとつにまとめてしまうことにします。

(a) AND回路
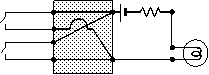
(b) OR回路

(c) NOT回路
(ハッチング部分がつなぎ方のパターンです)
図1-6 つなぎ方だけをまとめる
図1-6の回路は、これまで出てきた
AND回路、OR回路、NOT回路
と、つなぎ方が同じです。
このことを線のつなぎ方で確認しておきましょう。
![]()
![]()
色々な論理回路を作る際、つなぎ方をバラバラに考えるのは大変です。
そこで、図1-6のパターンは、既に分かっているものとします。
色々な演算を回路で表現してみましょう。
① X = C or ( A and B )
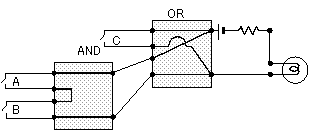
図1-7 C or (A
and B)
回路
表1-4 C or (A and
B)の真理値表
|
A |
B |
C |
A and B |
C or (A and B) |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
② X = not ( A or B )
この回路は、ORをNOTしたもので「NOR回路」と呼ばれます。
同じように、ANDをNOTしたものは「NAND回路」と呼ばれます。

図1-8 not(A or B) 回路
表1-5 not(A or B)回路の真理値表
|
A |
B |
A or B |
not (A or B) |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
図1-8を参考にしてNAND回路と真理値を作ってみましょう。
(ヒント:ORの部分をANDで入れかれるだけ)。
![]()
![]()
図1-6を観察してみましょう。ANDやORの出力に対して、
NOTのつなぎ方が少しだけ違っています。
実は、これが曲者でした。
例えば、X = not (not A)のつもりの下の回路を見てみましょう。
一見、正しそうに見えますが・・・。

図1-9 結線の論理回路で正しくない例(その1)
NOTは反転ですから、反転して反転ならば元に戻るはず。
表1-6が正しい結果です。
ですから、スイッチAを入れると、豆電球がつくはずなのに?
表1-6 not(not A)の真理値表
|
A |
not A |
X = not(not A) = A |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
これは、ANDとORの線の出し方と、
NOTの線の出し方が違っているためです。
実は、NOTが出力直前、すなわち乾電池と豆電球のすぐそばにないと、
正しい結果を出さないことがあります。
たとえば,次の例はうまくいきます。
真理値表の値と豆電球がつくかつかないを比較して、確認しましょう。
うまくいったり、うまくいかなかったり。困りましたね。
X = (not A) and (not B )
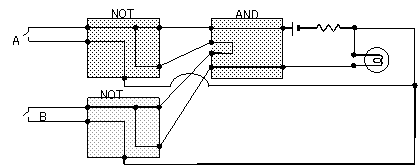
図1-10 結線の論理回路で正しい例
表1-5 (not A) and (not B)回路の真理値表
|
A |
B |
not A |
not B |
(not A) |
|
|
0 |
0 |
1 |
1 |
1 |
NOR回路と 同じであることに 注意しよう |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
しかし、ANDのところをORにしたら、とたんにうまくいきません。
これは、宿題として出しておきますので、
皆さんで確かめてみて下さい。
線のつなぎ方だけでNOTにするには、
スイッチと豆電球を並列に置くしかありません。
一方,ANDとORをつなぎ方は,豆電球と直列です。
ここが違っているわけです。
そこで、スイッチによる回路。次の章で、説明しましょう。
![]()
![]()
第1編 コンピュータの原理
 1. コンピュータは計算機
1. コンピュータは計算機
 2.コンピュータに必要な機能
2.コンピュータに必要な機能
第2編 論理回路の話
![]() 1.豆電球による論理回路
1.豆電球による論理回路
 2.スイッチによる論理回路
2.スイッチによる論理回路
 3.論理回路図の単純化
3.論理回路図の単純化
第3編 コンピュータの回路
 1.加算回路と減算回路
1.加算回路と減算回路
 2.記憶回路
2.記憶回路
 3.順序回路
3.順序回路
![]()
途中から,はじめるには
上の下線部をクリックします。