 
3.論理回路図の単純化
(ろんりかいろず の たんじゅんか)
3.1 論理回路を考えやすくするために
今まで、電磁石を使ったスイッチ(リレー)で論理回路を表現しましたが、
これで作ったコンピュータを「リレー計算機」と呼びます。
しかし、複雑な論理回路であるコンピュータを、
リレーで作るとなると、かなり大きくなってしまいます。
現在のコンピュータは、このスイッチを半導体で作っています。
形は違いますが、MOS集積回路(「もす しゅうせき かいろ」と読む)は、
原理的にはスイッチによる論理回路とまったく同じです。
今までは、動作のしくみを理解するために、
線の結び方や磁石の位置も分かる記号を使ってきました。
しかし、同じ動作をするのに、内部のしくみが違うというだけで、
回路図の形が違うのは困りものです。
テレビを見ようとするたとえを使ってみましょう。
内部のしくみが分からなくても、
テレビの操作方法さえ分かればテレビを見ることができます。
同じように、素子の中身がわからなくても、
素子がどんな動きをするのかさえ分かれば、
論理回路を考えることができます。
それでは、これまでの記号を単純化してみましょう。
 
3.2 回路記号の単純化
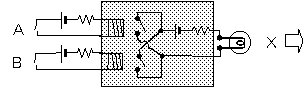
図2-6で示した図を、再び登場させました。
これらの回路図を観察してみましょう。
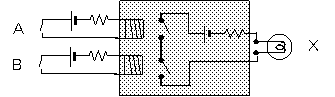
(a) AND回路
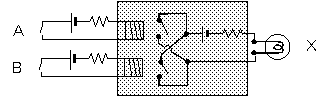
(b) OR回路

(c) NOT回路
まず、どの部分にも電源(乾電池と抵抗)が、必ず一組だけ入っています。
これは、あたりまえのこととして省略しましょう。
次に、入力側も出力側も、ひとつのオン/オフのデータに対して、
必ず2本線が出ています。
必ず2本だと分かっているのなら、これを1本線で済ませてしまいましょう。
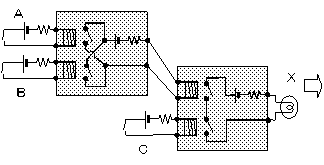
ハッチング部分は内部の構造を示しています。
電磁石を使ったスイッチ(リレー)による構造です。
これを半導体で構成すると別の図の形になります。
そこで、ハッチング部分、すなわち内部のしくみを表している部分は
忘れてしまうことにして、それぞれの働きを記号化することにします。
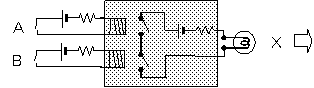
スイッチを入力、豆電球を出力にしましたが、
これらも別の形で実現しても構いません。
スイッチの替わりに温度を感知するセンサー、
豆電球の替わりに発光ダイオードなど、別のものを使っても構いません。
ただし、入力元や出力先は識別する必要がありますので、
それらを文字で表現します。
図3-1 AND/OR/NOTの記号
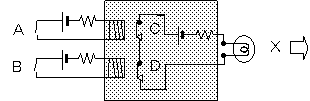
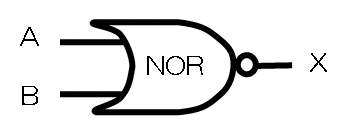
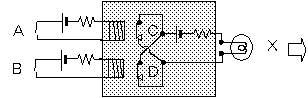
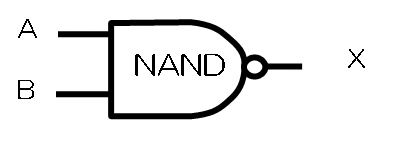
同じように、NOR、NANDについても記号化したものを図3-2に示します。
なお、素子の上に書いている「AND」、「OR」、「NOR」、「NAND」などは、
ふつうは書きません。
図3-2 NOR/NANDの記号
これまでに出てきた例を、以上の記号で描いてみましょう。
きっと、単純に表現できていることがわかるはずです。
図3-3 単純化された記号で論理回路を描く
 
|

 3.論理回路図の単純化
3.論理回路図の単純化





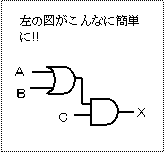
 1. コンピュータは計算機
1. コンピュータは計算機 2.コンピュータに必要な機能
2.コンピュータに必要な機能![]() 1.豆電球による論理回路
1.豆電球による論理回路 2.スイッチによる論理回路
2.スイッチによる論理回路 3.論理回路図の単純化
3.論理回路図の単純化 1.加算回路と減算回路
1.加算回路と減算回路 2.記憶回路
2.記憶回路 3.順序回路
3.順序回路![]()